Парадокс «Карусели истины» относится к классу самореферентных логических парадоксов. Он проявляется в цепочках утверждений, где каждое ссылается на истинность или ложность другого. Классический пример:

* А: «Б верно»
* Б: «В неверно»
* В: «А верно»

На первый взгляд, кажется, что любая попытка назначить истинность утверждениям приводит к противоречию: выбор истинности для одного утверждения автоматически вызывает несоответствие в другом, создавая бесконечный цикл — «карусель».

Классическая интерпретация парадокса

Традиционно такие парадоксы рассматриваются через бинарную логику, где истинность (True) и ложность (False) оцениваются как строгие противоположности. При попытке присвоить значения возникает противоречие:

* Предположим, что А истинно → тогда Б истинно → значит В ложно → следовательно, А ложно.
* Получается логическая петля, не позволяющая однозначно определить истинность.

Разрешение через логику импликации

Если рассмотреть классическую импликацию, где:

* True → False = False
* False → True = True

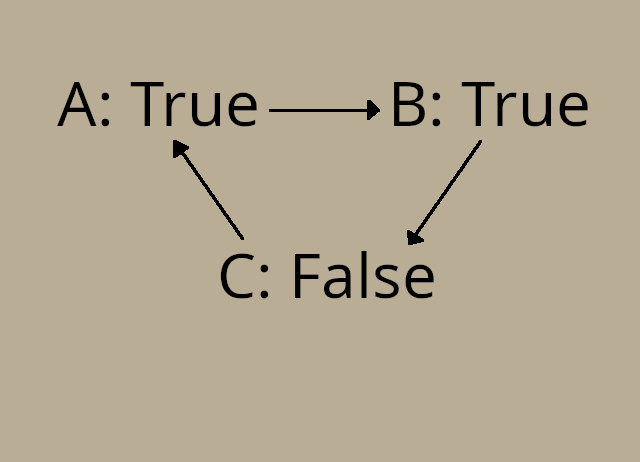
и допустить, что из ложного может следовать истина, ситуация меняется. Рассмотрим цепочку с присвоением В = ложь:

* В ложно.
* Тогда Б говорит «В неверно» → Б истинно (False → True = True).
* А говорит «Б верно» → А истинно (True → True = True).

Противоречия нет: цепочка стабилизируется. Ложь в В допускает истину в Б и А, и карусель перестаёт вращаться.

Вывод

Парадокс «Карусели истины» перестаёт быть парадоксом, если учитывать:

1. Ложь может быть первичной посылкой.
2. Классическая импликация допускает, что из ложного может следовать истина.

Таким образом, «карусель» не создает непреодолимого противоречия, а лишь показывает ограничения прямой бинарной логики при работе с самореферентными цепочками. Применение импликационной логики позволяет однозначно оценить истинность утверждений и «развязать» самореферентный цикл.