ФИЛОСОФСКОЕ
1
Почему False фундаментальнее True
---
ВОПРОС
Что первично — Истина или Ложь?
Любой математик скажет: Истина. Спросите его, откуда она — и он не ответит. Истина принимается как данность, как начало координат, как точка отсчёта. Ложь — отклонение, ошибка, отсутствие истины.
Но что если всё наоборот? Что если Ложь — это исходное состояние, а Истина — то, что из неё порождается?
Это не доказательство. Это набор независимых указаний из разных областей — логики, теории множеств, алгебры, онтологии и физики, — которые все направлены в одну сторону.
---
НАМЁК ПЕРВЫЙ: ИМПЛИКАЦИЯ
В классической логике импликация устроена асимметрично:
- False → True = True (из лжи может следовать истина)
- False → False = True (из лжи может следовать ложь)
- True → True = True (из истины следует истина)
- True → False = False (из истины НЕ может следовать ложь)
Из Лжи следует что угодно — и Ложь, и Истина. Ложь порождает оба значения. Истина порождает только себя. Ложь плодороднее. Это принцип ex falso quodlibet — из ложного следует всё.
Следствие, а не доказательство. Но направление ясно: Ложь — источник, Истина — результат.
---
НАМЁК ВТОРОЙ: ТОЖДЕСТВО
В алгебре логических операций тождественным элементом для XOR (настоящего «или») является False:
- A XOR False = A
False — это то, что не меняет. То, что было до операции. Нейтральный фон. Истина — это то, что переключает, изменяет, действует. Но чтобы действие произошло, нужен фон. Фон предшествует действию.
Ещё один намёк: False = ложь = ложь. Тождество лжи с собой порождает истину. Истина тождества лжи не порождает — она его не нарушает, но и не создаёт.
---
НАМЁК ТРЕТИЙ: ОРДИНАЛЫ ФОН НЕЙМАНА
В теории множеств натуральные числа строятся по фон Нейману:
- 0 = {} — пустое множество
- 1 = {{}} — множество, содержащее пустое множество
- 2 = {{}, {{}}} — и так далее
Пустое множество первично. Единица — это множество, содержащее пустоту. Без {} нет {{}}. Если {} соответствует False (ничто, отсутствие), а {{}} соответствует True (нечто, наличие), то False — строительный материал, из которого собирается True.
Без Лжи нет Истины. Обратное неверно — Истина не нужна для существования Лжи. Пустое множество существует само по себе.
---
НАМЁК ЧЕТВЁРТЫЙ: ОНТОЛОГИЯ
Заглянем за пределы логики — в начало.
До Большого взрыва не было ни пространства, ни времени, ни материи. Было Ничто — не пустота в пространстве, а отсутствие всего. Это {} в чистом виде — пустое множество без рамок.
Но Ничто не осталось Ничем. Что-то — пусть неизвестное нам, за гранью всего — не позволило пустоте остаться пустотой. {} породило {{}}. Появилось различение, а значит — Истина. Нечто возникло из Ничего.
И вот что важно: этот процесс необратим. Из Ничего возникло Нечто (False → True). Но Нечто не может вернуться в Ничто (True → False = False). Физика подтверждает это: закон сохранения энергии запрещает исчезновение в абсолютное ничто.
Логика копирует структуру мира. Импликация отражает онтологическую асимметрию: порождение идёт от пустоты к наполненности, но не обратно.
---
НАМЁК ПЯТЫЙ: БАНАХ-ТАРСКИЙ
Теорема Банаха-Тарского утверждает: шар в трёхмерном пространстве можно разрезать на конечное число частей и собрать из них два шара, идентичных исходному. Из одного — два. Из ничего (в смысле добавленной материи) — новое.
Все называют это парадоксом. Но это доказанная теорема — она верна.
Почему она кажется парадоксальной? Потому что мы мыслим изнутри рамок. Наш мир — это замкнутое множество {...}, в котором действуют законы сохранения: ничто не возникает из ничего, ничто не исчезает. Внутри рамок Банах-Тарский выглядит абсурдом.
Но теорема работает с актуальной бесконечностью — с бесконечным количеством точек нулевой меры. Каждая точка — это {}, ноль, ничто. Их бесконечно много. Без рамок они свободно перегруппируются, и из одного рождается два.
Это буквально тот же механизм: {} порождает {{}}. «Много ничего» создаёт новое. Парадокс Банаха-Тарского — не парадокс, а демонстрация свободного порождения без рамок.
---
СИСТЕМА
Пять независимых областей указывают в одну сторону:
Логика: из Лжи следует всё, из Истины — только Истина. Ложь — источник.
Алгебра: False — тождественный элемент, нейтральный фон, предшествующий действию.
Теория множеств: {} первично, {{}} вторично. Без пустоты нет наполненности.
Онтология: Ничто предшествует Нечто. Порождение необратимо.
Актуальная бесконечность: без рамок «много ничего» свободно порождает новое. Банах-Тарский — не парадокс, а норма безрамочного состояния.
---
ЗАЧЕМ?
Таблицы истинности не изменятся. Физика не сломается. Код не перепишется.
Но это и не про пользу. Это про правильное именование — про то же, что и ошибка OR/XOR. Мы неправильно расставляем иерархию: считаем Истину фундаментом, а Ложь — отклонением. На деле Ложь — это исходное состояние, из которого всё строится.
Зачем это видеть? Затем же, зачем видеть, что Земля вращается вокруг Солнца, а не наоборот. Расчёты Птолемея работали. Эпициклы давали правильные предсказания. Но когда Коперник поставил Солнце в центр — стало проще, яснее и красивее.
Красота — не украшение. Красота — это когда структура правильно отражает реальность.
---
ВОПРОС
Что первично — Истина или Ложь?
Любой математик скажет: Истина. Спросите его, откуда она — и он не ответит. Истина принимается как данность, как начало координат, как точка отсчёта. Ложь — отклонение, ошибка, отсутствие истины.
Но что если всё наоборот? Что если Ложь — это исходное состояние, а Истина — то, что из неё порождается?
Это не доказательство. Это набор независимых указаний из разных областей — логики, теории множеств, алгебры, онтологии и физики, — которые все направлены в одну сторону.
---
НАМЁК ПЕРВЫЙ: ИМПЛИКАЦИЯ
В классической логике импликация устроена асимметрично:
- False → True = True (из лжи может следовать истина)
- False → False = True (из лжи может следовать ложь)
- True → True = True (из истины следует истина)
- True → False = False (из истины НЕ может следовать ложь)
Из Лжи следует что угодно — и Ложь, и Истина. Ложь порождает оба значения. Истина порождает только себя. Ложь плодороднее. Это принцип ex falso quodlibet — из ложного следует всё.
Следствие, а не доказательство. Но направление ясно: Ложь — источник, Истина — результат.
---
НАМЁК ВТОРОЙ: ТОЖДЕСТВО
В алгебре логических операций тождественным элементом для XOR (настоящего «или») является False:
- A XOR False = A
False — это то, что не меняет. То, что было до операции. Нейтральный фон. Истина — это то, что переключает, изменяет, действует. Но чтобы действие произошло, нужен фон. Фон предшествует действию.
Ещё один намёк: False = ложь = ложь. Тождество лжи с собой порождает истину. Истина тождества лжи не порождает — она его не нарушает, но и не создаёт.
---
НАМЁК ТРЕТИЙ: ОРДИНАЛЫ ФОН НЕЙМАНА
В теории множеств натуральные числа строятся по фон Нейману:
- 0 = {} — пустое множество
- 1 = {{}} — множество, содержащее пустое множество
- 2 = {{}, {{}}} — и так далее
Пустое множество первично. Единица — это множество, содержащее пустоту. Без {} нет {{}}. Если {} соответствует False (ничто, отсутствие), а {{}} соответствует True (нечто, наличие), то False — строительный материал, из которого собирается True.
Без Лжи нет Истины. Обратное неверно — Истина не нужна для существования Лжи. Пустое множество существует само по себе.
---
НАМЁК ЧЕТВЁРТЫЙ: ОНТОЛОГИЯ
Заглянем за пределы логики — в начало.
До Большого взрыва не было ни пространства, ни времени, ни материи. Было Ничто — не пустота в пространстве, а отсутствие всего. Это {} в чистом виде — пустое множество без рамок.
Но Ничто не осталось Ничем. Что-то — пусть неизвестное нам, за гранью всего — не позволило пустоте остаться пустотой. {} породило {{}}. Появилось различение, а значит — Истина. Нечто возникло из Ничего.
И вот что важно: этот процесс необратим. Из Ничего возникло Нечто (False → True). Но Нечто не может вернуться в Ничто (True → False = False). Физика подтверждает это: закон сохранения энергии запрещает исчезновение в абсолютное ничто.
Логика копирует структуру мира. Импликация отражает онтологическую асимметрию: порождение идёт от пустоты к наполненности, но не обратно.
---
НАМЁК ПЯТЫЙ: БАНАХ-ТАРСКИЙ
Теорема Банаха-Тарского утверждает: шар в трёхмерном пространстве можно разрезать на конечное число частей и собрать из них два шара, идентичных исходному. Из одного — два. Из ничего (в смысле добавленной материи) — новое.
Все называют это парадоксом. Но это доказанная теорема — она верна.
Почему она кажется парадоксальной? Потому что мы мыслим изнутри рамок. Наш мир — это замкнутое множество {...}, в котором действуют законы сохранения: ничто не возникает из ничего, ничто не исчезает. Внутри рамок Банах-Тарский выглядит абсурдом.
Но теорема работает с актуальной бесконечностью — с бесконечным количеством точек нулевой меры. Каждая точка — это {}, ноль, ничто. Их бесконечно много. Без рамок они свободно перегруппируются, и из одного рождается два.
Это буквально тот же механизм: {} порождает {{}}. «Много ничего» создаёт новое. Парадокс Банаха-Тарского — не парадокс, а демонстрация свободного порождения без рамок.
---
СИСТЕМА
Пять независимых областей указывают в одну сторону:
Логика: из Лжи следует всё, из Истины — только Истина. Ложь — источник.
Алгебра: False — тождественный элемент, нейтральный фон, предшествующий действию.
Теория множеств: {} первично, {{}} вторично. Без пустоты нет наполненности.
Онтология: Ничто предшествует Нечто. Порождение необратимо.
Актуальная бесконечность: без рамок «много ничего» свободно порождает новое. Банах-Тарский — не парадокс, а норма безрамочного состояния.
---
ЗАЧЕМ?
Таблицы истинности не изменятся. Физика не сломается. Код не перепишется.
Но это и не про пользу. Это про правильное именование — про то же, что и ошибка OR/XOR. Мы неправильно расставляем иерархию: считаем Истину фундаментом, а Ложь — отклонением. На деле Ложь — это исходное состояние, из которого всё строится.
Зачем это видеть? Затем же, зачем видеть, что Земля вращается вокруг Солнца, а не наоборот. Расчёты Птолемея работали. Эпициклы давали правильные предсказания. Но когда Коперник поставил Солнце в центр — стало проще, яснее и красивее.
Красота — не украшение. Красота — это когда структура правильно отражает реальность.
Актуальная бесконечность — понятие, введённое Георгом Кантором, утверждающее что бесконечное множество существует целиком, как завершённый объект. Из этого постулата следуют результаты, которые принято называть парадоксами: Банаха-Тарского (из одного шара можно сложить два таких же), необходимость аксиомы выбора (утверждение существования без описания), разные «размеры» бесконечности (одних бесконечностей «больше» чем других).
Предлагается альтернативный класс бесконечности, в котором эти вопросы не возникают.
ОПРЕДЕЛЕНИЕ
Псевдобесконечность (П) — класс бесконечности, который конечен в каждый момент обращения, но не имеет достижимого предела. Актуальная бесконечность является недостижимым пределом псевдобесконечности.
Свойства:
Конечность состояния — в каждый момент количество порождённых элементов конечно.
Неограниченность — для любого порождённого элемента существует следующий.
Детерминированность — повторный запрос к тому же элементу даёт тот же результат.
Причинность — каждый элемент порождён в результате запроса, ничто не существует без причины.
Недостижимость предела — актуальная бесконечность является пределом, к которому псевдобесконечность стремится, но никогда не достигает. Парадоксы актуальной бесконечности существуют в этом пределе и именно поэтому нереализуемы.
АНАЛОГИЯ
Компьютерная игра с процедурной генерацией миров. В памяти хранится не триллион миров, а правило их порождения. Пришёл в мир — он построился. Ушёл — его нет. Вернулся — он тот же самый. Миров потенциально бесконечно, но актуально существует только тот, в который ты смотришь.
Как говорил Эйнштейн: «Вы что, действительно уверены, что когда вы не смотрите на Луну, её нет?» Для псевдобесконечности ответ — да. Элемент существует когда к нему обратились.
ОТНОШЕНИЕ К АКТУАЛЬНОЙ БЕСКОНЕЧНОСТИ
П не отменяет А и не опровергает её. Это другая система с другими правилами, подобно тому как геометрия Лобачевского не отменяет геометрию Евклида.
В А парадоксы (Банаха-Тарского, аксиома выбора, разные мощности) существуют как свойства завершённой бесконечности. В П эти парадоксы существуют в недостижимом пределе — они реальны, но нереализуемы, как горизонт, который видишь, но до которого не дойдёшь.
Аксиома выбора в П не нужна — выбор делается по одному элементу в момент порождения. Всегда конечный шаг, всегда обоснованный.
Диагональный аргумент Кантора в П означает не «вещественных больше чем натуральных», а «процесс порождения не завершён» — что верно по определению. На любом конкретном размере биекция между натуральными и вещественными строится.
СЛЕДСТВИЯ
Вся конструктивная математика полностью сохраняется в П. Всё что реально доказано — доказано конечным числом шагов. Каждое вычисление конечно. Интегралы, пределы, ряды — всё работает через конечные приближения нужной точности.
П предлагает систему, в которой можно работать с неограниченными процессами без необходимости постулировать завершённую бесконечность и без парадоксов, которые из этого постулата следуют.
ВЫВОД
Псевдобесконечность — не замена актуальной бесконечности, а альтернативная система рядом с ней. Она конечна, детерминирована, воспроизводима, причинно-следственна и порождается по запросу. В ней сохраняется вся мощь конструктивной математики, а парадоксы актуальной бесконечности существуют только в недостижимом пределе.
Предлагается альтернативный класс бесконечности, в котором эти вопросы не возникают.
ОПРЕДЕЛЕНИЕ
Псевдобесконечность (П) — класс бесконечности, который конечен в каждый момент обращения, но не имеет достижимого предела. Актуальная бесконечность является недостижимым пределом псевдобесконечности.
Свойства:
Конечность состояния — в каждый момент количество порождённых элементов конечно.
Неограниченность — для любого порождённого элемента существует следующий.
Детерминированность — повторный запрос к тому же элементу даёт тот же результат.
Причинность — каждый элемент порождён в результате запроса, ничто не существует без причины.
Недостижимость предела — актуальная бесконечность является пределом, к которому псевдобесконечность стремится, но никогда не достигает. Парадоксы актуальной бесконечности существуют в этом пределе и именно поэтому нереализуемы.
АНАЛОГИЯ
Компьютерная игра с процедурной генерацией миров. В памяти хранится не триллион миров, а правило их порождения. Пришёл в мир — он построился. Ушёл — его нет. Вернулся — он тот же самый. Миров потенциально бесконечно, но актуально существует только тот, в который ты смотришь.
Как говорил Эйнштейн: «Вы что, действительно уверены, что когда вы не смотрите на Луну, её нет?» Для псевдобесконечности ответ — да. Элемент существует когда к нему обратились.
ОТНОШЕНИЕ К АКТУАЛЬНОЙ БЕСКОНЕЧНОСТИ
П не отменяет А и не опровергает её. Это другая система с другими правилами, подобно тому как геометрия Лобачевского не отменяет геометрию Евклида.
В А парадоксы (Банаха-Тарского, аксиома выбора, разные мощности) существуют как свойства завершённой бесконечности. В П эти парадоксы существуют в недостижимом пределе — они реальны, но нереализуемы, как горизонт, который видишь, но до которого не дойдёшь.
Аксиома выбора в П не нужна — выбор делается по одному элементу в момент порождения. Всегда конечный шаг, всегда обоснованный.
Диагональный аргумент Кантора в П означает не «вещественных больше чем натуральных», а «процесс порождения не завершён» — что верно по определению. На любом конкретном размере биекция между натуральными и вещественными строится.
СЛЕДСТВИЯ
Вся конструктивная математика полностью сохраняется в П. Всё что реально доказано — доказано конечным числом шагов. Каждое вычисление конечно. Интегралы, пределы, ряды — всё работает через конечные приближения нужной точности.
П предлагает систему, в которой можно работать с неограниченными процессами без необходимости постулировать завершённую бесконечность и без парадоксов, которые из этого постулата следуют.
ВЫВОД
Псевдобесконечность — не замена актуальной бесконечности, а альтернативная система рядом с ней. Она конечна, детерминирована, воспроизводима, причинно-следственна и порождается по запросу. В ней сохраняется вся мощь конструктивной математики, а парадоксы актуальной бесконечности существуют только в недостижимом пределе.
Логические операторы и метаязык
В формальной логике и языках программирования существует фундаментальная ошибка именования, которая тянется уже более ста лет и влияет на мышление миллионов программистов.
ПРОБЛЕМА
В естественном языке (метаязыке) слово «или» всегда означает выбор одного из двух:
«Ты идёшь налево или направо?» — не оба сразу.
«Это правда или ложь?» — не обе сразу.
«Будешь чай или кофе?» — одно из двух.
Однако в формальной логике оператор OR (ИЛИ) означает нечто другое — «хотя бы одно из двух, возможно оба». А то, что в метаязыке является настоящим «или», спрятано под непроизносимым именем XOR (исключающее ИЛИ).
ЧТО ТАКОЕ OR НА САМОМ ДЕЛЕ?
OR — это не «или». OR — это запятая.
«Купи хлеб, молоко, масло» — перечисление через запятую. Может купишь одно, может два, может всё. Любая комбинация, кроме «ничего из списка». Это в точности таблица истинности OR: ложь только когда всё ложно.
ПРАВИЛЬНОЕ СООТВЕТСТВИЕ
В метаязыке «и» (оба) — это оператор конъюнкции. Текущее имя AND. Предлагаемое имя AND. Здесь ошибки нет.
В метаязыке «,» (запятая, перечисление) — это оператор дизъюнкции. Текущее имя OR. Предлагаемое имя COM (от comma — запятая).
В метаязыке «или» (одно из двух) — это оператор исключающего или. Текущее имя XOR. Предлагаемое имя OR.
СЛЕДСТВИЯ
Программисты пишут if (a || b) и if (a && b) — это 99% всего кода. XOR почти не используется в бизнес-логике, хотя множество задач — это именно исключающий выбор: «пользователь либо админ, либо гость», «заказ либо оплачен, либо отменён», «свет либо включён, либо выключен».
Вместо одного оператора XOR программист пишет (a || b) && !(a && b) — лишний код, лишняя сложность, лишние ошибки. Когда XOR был добавлен в аппаратную часть компьютеров, производительность выросла на 30%, потому что одна операция заменила цепочку из трёх.
ВЫВОД
Формальная логика назвала OR словом «или», хотя это запятая. А настоящее «или» назвала XOR и спрятала за непроизносимой аббревиатурой. Эта ошибка именования живёт уже более века и ежедневно порождает избыточный код по всему миру.
Исправление: COM (comma) вместо OR, OR вместо XOR. Три оператора — три имени — каждое соответствует тому, как мыслит человек.
В формальной логике и языках программирования существует фундаментальная ошибка именования, которая тянется уже более ста лет и влияет на мышление миллионов программистов.
ПРОБЛЕМА
В естественном языке (метаязыке) слово «или» всегда означает выбор одного из двух:
«Ты идёшь налево или направо?» — не оба сразу.
«Это правда или ложь?» — не обе сразу.
«Будешь чай или кофе?» — одно из двух.
Однако в формальной логике оператор OR (ИЛИ) означает нечто другое — «хотя бы одно из двух, возможно оба». А то, что в метаязыке является настоящим «или», спрятано под непроизносимым именем XOR (исключающее ИЛИ).
ЧТО ТАКОЕ OR НА САМОМ ДЕЛЕ?
OR — это не «или». OR — это запятая.
«Купи хлеб, молоко, масло» — перечисление через запятую. Может купишь одно, может два, может всё. Любая комбинация, кроме «ничего из списка». Это в точности таблица истинности OR: ложь только когда всё ложно.
ПРАВИЛЬНОЕ СООТВЕТСТВИЕ
В метаязыке «и» (оба) — это оператор конъюнкции. Текущее имя AND. Предлагаемое имя AND. Здесь ошибки нет.
В метаязыке «,» (запятая, перечисление) — это оператор дизъюнкции. Текущее имя OR. Предлагаемое имя COM (от comma — запятая).
В метаязыке «или» (одно из двух) — это оператор исключающего или. Текущее имя XOR. Предлагаемое имя OR.
СЛЕДСТВИЯ
Программисты пишут if (a || b) и if (a && b) — это 99% всего кода. XOR почти не используется в бизнес-логике, хотя множество задач — это именно исключающий выбор: «пользователь либо админ, либо гость», «заказ либо оплачен, либо отменён», «свет либо включён, либо выключен».
Вместо одного оператора XOR программист пишет (a || b) && !(a && b) — лишний код, лишняя сложность, лишние ошибки. Когда XOR был добавлен в аппаратную часть компьютеров, производительность выросла на 30%, потому что одна операция заменила цепочку из трёх.
ВЫВОД
Формальная логика назвала OR словом «или», хотя это запятая. А настоящее «или» назвала XOR и спрятала за непроизносимой аббревиатурой. Эта ошибка именования живёт уже более века и ежедневно порождает избыточный код по всему миру.
Исправление: COM (comma) вместо OR, OR вместо XOR. Три оператора — три имени — каждое соответствует тому, как мыслит человек.
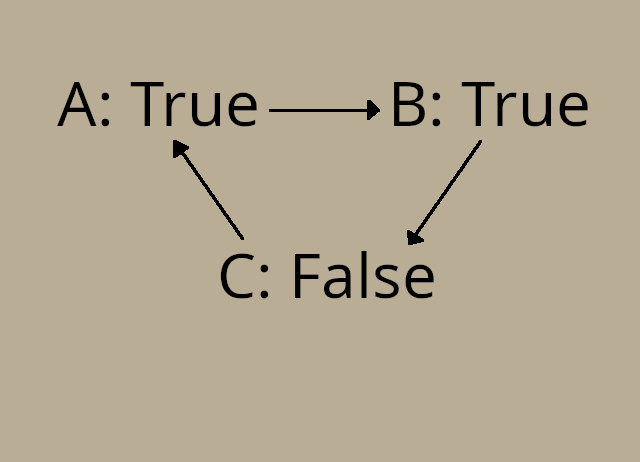
Парадокс «Карусели истины» относится к классу самореферентных логических парадоксов. Он проявляется в цепочках утверждений, где каждое ссылается на истинность или ложность другого. Классический пример:
* А: «Б верно»
* Б: «В неверно»
* В: «А верно»
На первый взгляд, кажется, что любая попытка назначить истинность утверждениям приводит к противоречию: выбор истинности для одного утверждения автоматически вызывает несоответствие в другом, создавая бесконечный цикл — «карусель».
Классическая интерпретация парадокса
Традиционно такие парадоксы рассматриваются через бинарную логику, где истинность (True) и ложность (False) оцениваются как строгие противоположности. При попытке присвоить значения возникает противоречие:
* Предположим, что А истинно → тогда Б истинно → значит В ложно → следовательно, А ложно.
* Получается логическая петля, не позволяющая однозначно определить истинность.
Разрешение через логику импликации
Если рассмотреть классическую импликацию, где:
* True → False = False
* False → True = True
и допустить, что из ложного может следовать истина, ситуация меняется. Рассмотрим цепочку с присвоением В = ложь:
* В ложно.
* Тогда Б говорит «В неверно» → Б истинно (False → True = True).
* А говорит «Б верно» → А истинно (True → True = True).
Противоречия нет: цепочка стабилизируется. Ложь в В допускает истину в Б и А, и карусель перестаёт вращаться.
Вывод
Парадокс «Карусели истины» перестаёт быть парадоксом, если учитывать:
1. Ложь может быть первичной посылкой.
2. Классическая импликация допускает, что из ложного может следовать истина.
Таким образом, «карусель» не создает непреодолимого противоречия, а лишь показывает ограничения прямой бинарной логики при работе с самореферентными цепочками. Применение импликационной логики позволяет однозначно оценить истинность утверждений и «развязать» самореферентный цикл.
* А: «Б верно»
* Б: «В неверно»
* В: «А верно»
На первый взгляд, кажется, что любая попытка назначить истинность утверждениям приводит к противоречию: выбор истинности для одного утверждения автоматически вызывает несоответствие в другом, создавая бесконечный цикл — «карусель».
Классическая интерпретация парадокса
Традиционно такие парадоксы рассматриваются через бинарную логику, где истинность (True) и ложность (False) оцениваются как строгие противоположности. При попытке присвоить значения возникает противоречие:
* Предположим, что А истинно → тогда Б истинно → значит В ложно → следовательно, А ложно.
* Получается логическая петля, не позволяющая однозначно определить истинность.
Разрешение через логику импликации
Если рассмотреть классическую импликацию, где:
* True → False = False
* False → True = True
и допустить, что из ложного может следовать истина, ситуация меняется. Рассмотрим цепочку с присвоением В = ложь:
* В ложно.
* Тогда Б говорит «В неверно» → Б истинно (False → True = True).
* А говорит «Б верно» → А истинно (True → True = True).
Противоречия нет: цепочка стабилизируется. Ложь в В допускает истину в Б и А, и карусель перестаёт вращаться.
Вывод
Парадокс «Карусели истины» перестаёт быть парадоксом, если учитывать:
1. Ложь может быть первичной посылкой.
2. Классическая импликация допускает, что из ложного может следовать истина.
Таким образом, «карусель» не создает непреодолимого противоречия, а лишь показывает ограничения прямой бинарной логики при работе с самореферентными цепочками. Применение импликационной логики позволяет однозначно оценить истинность утверждений и «развязать» самореферентный цикл.
Введение
Парадокс лампы Томпсона показывает, как бесконечное деление процесса создаёт математическую неопределённость. Формально, после бесконечного числа переключений лампа одновременно и горит, и не горит. Математика фиксирует лишь стремление ряда к пределу, но сама последовательность переключений бесконечна.
Бесконечная последовательность и вероятность
Представим лампу, изначально выключенную, которая переключается на каждом шаге бесконечной последовательности. Время между шагами делится по геометрической прогрессии: 1/2, 1/4, 1/8 и так далее.
Шаги с нечётными номерами дают лампе шанс быть включённой.
Шаги с чётными номерами дают лампе шанс быть выключенной.
Вычисление вероятностей
Для включённой лампы сумма шансов по шагам с нечётными номерами:
S_on = 1/2 + 1/8 + 1/32 + ...
Это геометрическая прогрессия с первым членом a = 1/2 и знаменателем q = 1/4:
S_on = a / (1 - q) = (1/2) / (1 - 1/4) = 2/3
Для выключенной лампы сумма шансов по шагам с чётными номерами:
S_off = 1/4 + 1/16 + 1/64 + ...
Геометрическая прогрессия с a = 1/4 и q = 1/4:
S_off = a / (1 - q) = (1/4) / (1 - 1/4) = 1/3
Вывод
Даже при бесконечной последовательности можно определить конкретные шансы на состояние лампы:
вероятность быть включённой — 2/3
вероятность быть выключенной — 1/3
Хотя мы никогда не дойдём до конечного шага, математическая структура процесса позволяет придать смысл бесконечной последовательности через вероятности.
Парадокс лампы Томпсона показывает, как бесконечное деление процесса создаёт математическую неопределённость. Формально, после бесконечного числа переключений лампа одновременно и горит, и не горит. Математика фиксирует лишь стремление ряда к пределу, но сама последовательность переключений бесконечна.
Бесконечная последовательность и вероятность
Представим лампу, изначально выключенную, которая переключается на каждом шаге бесконечной последовательности. Время между шагами делится по геометрической прогрессии: 1/2, 1/4, 1/8 и так далее.
Шаги с нечётными номерами дают лампе шанс быть включённой.
Шаги с чётными номерами дают лампе шанс быть выключенной.
Вычисление вероятностей
Для включённой лампы сумма шансов по шагам с нечётными номерами:
S_on = 1/2 + 1/8 + 1/32 + ...
Это геометрическая прогрессия с первым членом a = 1/2 и знаменателем q = 1/4:
S_on = a / (1 - q) = (1/2) / (1 - 1/4) = 2/3
Для выключенной лампы сумма шансов по шагам с чётными номерами:
S_off = 1/4 + 1/16 + 1/64 + ...
Геометрическая прогрессия с a = 1/4 и q = 1/4:
S_off = a / (1 - q) = (1/4) / (1 - 1/4) = 1/3
Вывод
Даже при бесконечной последовательности можно определить конкретные шансы на состояние лампы:
вероятность быть включённой — 2/3
вероятность быть выключенной — 1/3
Хотя мы никогда не дойдём до конечного шага, математическая структура процесса позволяет придать смысл бесконечной последовательности через вероятности.
Введение
В диалоге Льюиса Кэрролла, известном как «парадокс черепахи», черепаха требует от собеседника не просто доказать импликацию A⇒B, а доказать, что из предпосылки A следует сама эта импликация — то есть требует бесконечно продолжать доказательство каждого шага. Это ведёт к бесконечному регрессу и парадоксу.
Парадокс
Человек утверждает: «Если A, то B» — A⇒B.
Черепаха не принимает это как аксиому и просит доказать, что из A следует импликация A⇒B:
A⊢(A⇒B)
В ответ она снова требует доказать, что из A следует, что из A следует A⇒B, и так далее — бесконечно.
Рассмотрение импликации через таблицу истинности
Импликация A⇒B истинна в трёх из четырёх случаев:
Истина → Истина — импликация истинна.
Истина → Ложь — импликация ложна (единственный случай ложности).
Ложь → Истина — импликация истинна.
Ложь → Ложь — импликация истинна.
Это значит:
В трёх случаях доказывать импликацию не требуется — она автоматически истинна.
В одном случае (Истина → Ложь) доказать импликацию невозможно, так как она ложна.
Заключение
Парадокс черепахи возникает из-за попытки доказать импликацию там, где это либо не нужно, либо невозможно. Постоянное требование новых доказательств создаёт бесконечный регресс.
Решение — признать импликацию и правила вывода (например, модус поненс) как базовые аксиомы логики. Это останавливает регресс и позволяет строить корректные доказательства.
Таким образом, парадокс Кэрролла демонстрирует важность принятия фундаментальных логических правил, без которых рассуждение становится бесконечным и неработающим.
В диалоге Льюиса Кэрролла, известном как «парадокс черепахи», черепаха требует от собеседника не просто доказать импликацию A⇒B, а доказать, что из предпосылки A следует сама эта импликация — то есть требует бесконечно продолжать доказательство каждого шага. Это ведёт к бесконечному регрессу и парадоксу.
Парадокс
Человек утверждает: «Если A, то B» — A⇒B.
Черепаха не принимает это как аксиому и просит доказать, что из A следует импликация A⇒B:
A⊢(A⇒B)
В ответ она снова требует доказать, что из A следует, что из A следует A⇒B, и так далее — бесконечно.
Рассмотрение импликации через таблицу истинности
Импликация A⇒B истинна в трёх из четырёх случаев:
Истина → Истина — импликация истинна.
Истина → Ложь — импликация ложна (единственный случай ложности).
Ложь → Истина — импликация истинна.
Ложь → Ложь — импликация истинна.
Это значит:
В трёх случаях доказывать импликацию не требуется — она автоматически истинна.
В одном случае (Истина → Ложь) доказать импликацию невозможно, так как она ложна.
Заключение
Парадокс черепахи возникает из-за попытки доказать импликацию там, где это либо не нужно, либо невозможно. Постоянное требование новых доказательств создаёт бесконечный регресс.
Решение — признать импликацию и правила вывода (например, модус поненс) как базовые аксиомы логики. Это останавливает регресс и позволяет строить корректные доказательства.
Таким образом, парадокс Кэрролла демонстрирует важность принятия фундаментальных логических правил, без которых рассуждение становится бесконечным и неработающим.
Традиционная логика утверждает существование четырёх основных законов: тождества, непротиворечия, исключённого третьего и достаточного основания.
Однако внимательный анализ показывает, что избыточны все, кроме одного — закона достаточного основания. Более того, первые три закона — в правильном порядке — охватываются и выводятся из него.
Закон достаточного основания
P истинно ⟹ ∃Q(Q истинно ⟹ P)
Истинно только то, что имеет основание.
Этот закон связывает логику с реальностью: любое утверждение должно быть выведено, доказано или иметь опору в аксиоме, опыте или другой истине.
Без него логика превращается в игру символов, лишённую смысла.
Следствия из закона достаточного основания:
1. Закон тождества (P ⟹ P)
Берём P как своё же основание: Q = P.
Тогда по ЗДС: «P истинно ⟹ P истинно».
Вывод: закон тождества — частный случай ЗДС.
2. Закон непротиворечия ¬(P ∧ ¬P)
Предположим, что P и ¬P истинны одновременно.
Тогда им нужны основания Q₁ и Q₂ для P и ¬P.
Но никакое основание не может одновременно выводить P и ¬P, иначе оно противоречиво.
Вывод: ¬(P ∧ ¬P) следует из невозможности иметь обоснование одновременно для P и ¬P.
3. Закон исключённого третьего P ∨ ¬P
Если ни P, ни ¬P не имеют основания, то по ЗДС оба не истинны.
Но для каждого утверждения должно быть основание для истинности.
Следовательно, хотя бы одно из P или ¬P должно иметь основание.
Вывод: P ∨ ¬P.
Таким образом, классические три закона оказываются частными случаями единственного закона достаточного основания.
Вывод:
Все остальные законы логики — производные одного, который обеспечивает обоснованность и содержание.
Он образует надёжный фундамент для любой строгой логической системы.
Однако внимательный анализ показывает, что избыточны все, кроме одного — закона достаточного основания. Более того, первые три закона — в правильном порядке — охватываются и выводятся из него.
Закон достаточного основания
P истинно ⟹ ∃Q(Q истинно ⟹ P)
Истинно только то, что имеет основание.
Этот закон связывает логику с реальностью: любое утверждение должно быть выведено, доказано или иметь опору в аксиоме, опыте или другой истине.
Без него логика превращается в игру символов, лишённую смысла.
Следствия из закона достаточного основания:
1. Закон тождества (P ⟹ P)
Берём P как своё же основание: Q = P.
Тогда по ЗДС: «P истинно ⟹ P истинно».
Вывод: закон тождества — частный случай ЗДС.
2. Закон непротиворечия ¬(P ∧ ¬P)
Предположим, что P и ¬P истинны одновременно.
Тогда им нужны основания Q₁ и Q₂ для P и ¬P.
Но никакое основание не может одновременно выводить P и ¬P, иначе оно противоречиво.
Вывод: ¬(P ∧ ¬P) следует из невозможности иметь обоснование одновременно для P и ¬P.
3. Закон исключённого третьего P ∨ ¬P
Если ни P, ни ¬P не имеют основания, то по ЗДС оба не истинны.
Но для каждого утверждения должно быть основание для истинности.
Следовательно, хотя бы одно из P или ¬P должно иметь основание.
Вывод: P ∨ ¬P.
Таким образом, классические три закона оказываются частными случаями единственного закона достаточного основания.
Вывод:
Все остальные законы логики — производные одного, который обеспечивает обоснованность и содержание.
Он образует надёжный фундамент для любой строгой логической системы.
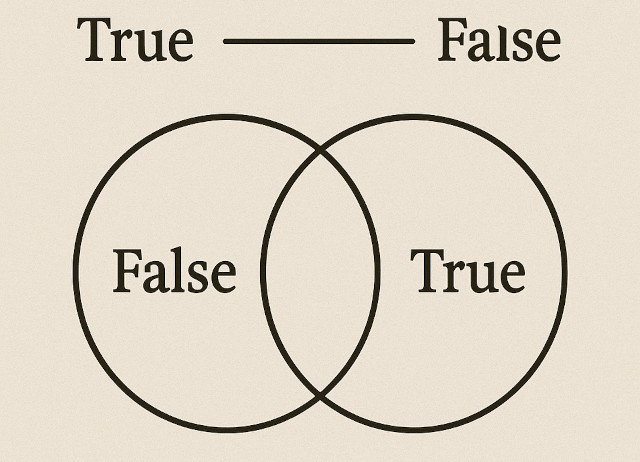
«В классической логике импликация допускает, что из ложной посылки может следовать истина (False → True истинно), тогда как из истины ложь следовать не может (True → False ложно). Это указывает на возможную первичность лжи как исходной посылки, из которой может быть выведена истина. Истина в этом контексте не является абсолютным началом, а выступает как результат логической конструкции, начинающейся с ложности. Таким образом, ложь можно рассматривать как более фундаментальное основание в структуре логического следования.»
Парадокс лжеца традиционно воспринимается как непреодолимое логическое противоречие, порождаемое утверждением «Это высказывание ложно». Однако можно рассмотреть эту проблему через призму современной логики импликации. Если принять утверждение за истинное, то из него следует, что оно ложно (True → False). Согласно таблице истинности импликации, такая ситуация невозможна, что выводит утверждение за рамки истинных высказываний и относит его к ложным.
Если же предположить, что утверждение ложно, то его содержимое («Это высказывание ложно») приводит к истинности, что не противоречит закону импликации. Таким образом, возникает импликация False → True, которая по таблице истинности истинна (True). Но на этом всё и заканчивается, так как из этой истинности по закону импликации уже не может следовать ложь. Следовательно, утверждение остаётся ложным, и противоречия не возникает.
А следовательно, «парадокс» исчезает как парадокс в классическом смысле и превращается в результат некорректного ожидания однозначной истинности высказывания, которое по своей природе является ложным. Таким образом, лжец не создаёт парадокса, а указывает на границы применимости классических истинностных оценок к самореферентным высказываниям.
Если же предположить, что утверждение ложно, то его содержимое («Это высказывание ложно») приводит к истинности, что не противоречит закону импликации. Таким образом, возникает импликация False → True, которая по таблице истинности истинна (True). Но на этом всё и заканчивается, так как из этой истинности по закону импликации уже не может следовать ложь. Следовательно, утверждение остаётся ложным, и противоречия не возникает.
А следовательно, «парадокс» исчезает как парадокс в классическом смысле и превращается в результат некорректного ожидания однозначной истинности высказывания, которое по своей природе является ложным. Таким образом, лжец не создаёт парадокса, а указывает на границы применимости классических истинностных оценок к самореферентным высказываниям.
1
